ML Notes

Machine Learning (supervised learning) notes

Use of algorithms and statistical models to perform tasks without explicit instructions, instead using patterns and inference.

Examples:

import matplotlib.pyplot as plt
import numpy as np

Matplotlib:

Practical Example - Plotting

# Effect of time spent walking (hours) on the distance travelled (miles)
time_spent_walking = [1, 2, 3, 4, 5]  # (independent variable)
distance = [2, 4, 6, 8, 10]  # (dependent variable)

plt.plot(time_spent_walking, distance)
plt.xlabel("Time Spent Walking (hours)")
plt.ylabel("Distance (miles)")
plt.title("Effect of time spent walking on distance travelled")
plt.show()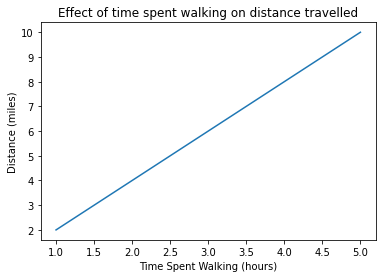

# Effect of car age (years) on price ($)
car_age = [1, 2, 5, 10, 30]
price = [30000, 25000, 18000, 10000, 4000]

plt.plot(car_age, price)
plt.xlabel("Car Age (years)")
plt.ylabel("Price ($)")
plt.title("Effect of car age on price")
plt.show()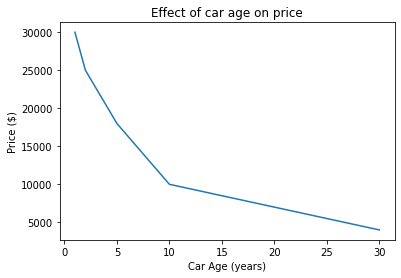

# Effect of amount of time spent studying (hours) on test score results (%)
study_time = [1, 5, 10, 20, 50, 100]
test_score_results = [40, 60, 70, 75, 88, 93]

plt.plot(study_time, test_score_results)
plt.xlabel("Study Time (hours)")
plt.ylabel("Test Score (%)")
plt.title("Effect of study time on test scores")
plt.show()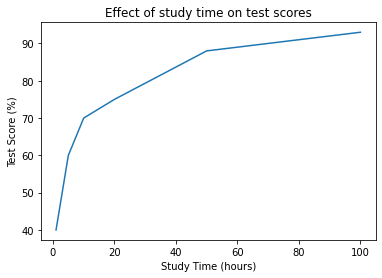

Linear Regression: y = mx + b

  • x: x axis
  • y: y axis
  • m: gradient of line
  • b: value of y when x = 0

Example 1

x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]

plt.plot(x, y)
plt.show()

# y = 2x + 2
for i in x:
    y = 2 * i
    print(y)
2
4
6
8
10

Example 2

x = [1, 2, 3, 4, 5]
y = [6, 9, 12, 15, 18]

plt.plot(x, y)
plt.show()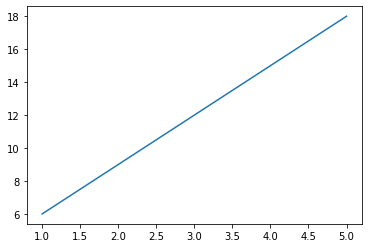

# y = mx + b
for i in x:
    y = (3 * i) + 3
    print(y)
6
9
12
15
18

Example 3

x = [0, 1, 2, 3, 4]
y = [6, 9, 12, 15, 18]

plt.plot(x, y)
plt.show()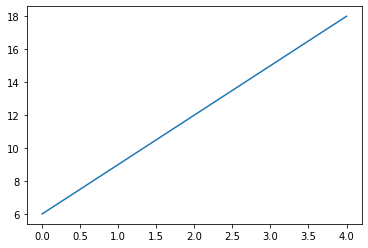

# y = mx + b
# y = 3x + 6

for i in x:
    y = (3 * i) + 6
    print(i, y)
0 6
1 9
2 12
3 15
4 18

Practical Examples - Linear Regression (y = mx + b)

Question 1

# Effect of amount of water provided (L) per day on size of trees (m)
water = [0, 1, 2, 3, 4, 5, 6, 7, 8]
tree_size = [4, 5, 6, 7, 8, 9, 10, 11, 12]

plt.plot(water, tree_size)
plt.show()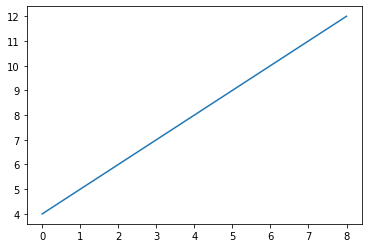

Solution

# y = mx + b
for x in water:
    y = (1 * x) + 4
    print(x, y)
    # y = x + 4
0 4
1 5
2 6
3 7
4 8
5 9
6 10
7 11
8 12

Question 2

# Effect of wingspan (cm) on flying speed (km/h)
wingspan = [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
flying_speed = [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50]
plt.plot(wingspan, flying_speed)
plt.show()

Solution

# y = mx + b
for x in wingspan:
    y = 0.5 * x
    print(x, y)
    # y = 0.5x + 0
0 0.0
10 5.0
20 10.0
30 15.0
40 20.0
50 25.0
60 30.0
70 35.0
80 40.0
90 45.0
100 50.0

Question 3

# Effect of number of gifts given to employees each year, on staff statisfaction levels (100%)
num_of_gifts = [0, 1, 2, 3, 4, 5]
satisfaction = [50, 55, 60, 65, 70, 75]
plt.plot(num_of_gifts, satisfaction)
plt.show()

Solution

# y = mx + b
for x in num_of_gifts:
    y = (5 * x) + 50
    print(x, y)
    # y = 5x + 50
0 50
1 55
2 60
3 65
4 70
5 75

Line of Best Fit

Cost: distance of each point from best fit line

Loss: Sum of all distances between best fit line and data points (sum of costs)

image.png

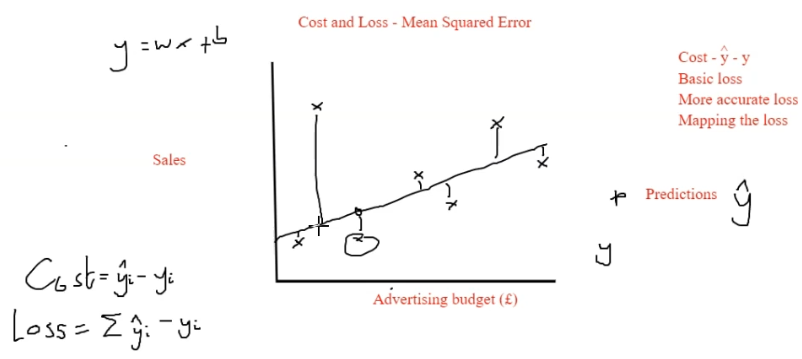
Mean Squared Error (MSE)

image.png

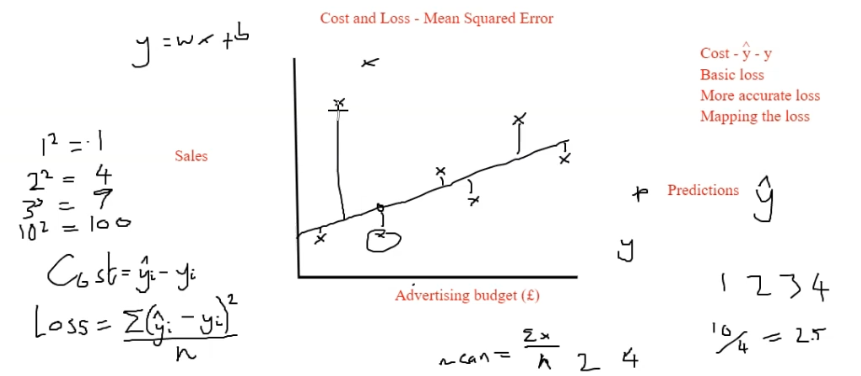
Mean Squared Error = sum (Y @ prediction - y at datapoint)^2 / number of datapoints

Example

# Data
x_data = [1, 5, 8, 10]
y_data = [4, 8, 9, 7]

# Data plot
plt.plot(x_data, y_data)
plt.show()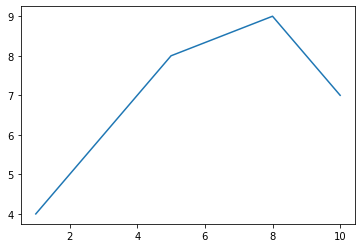

Best fit line (y = mx + b)

# Calculate m, b
m, b = np.polyfit(x_data, y_data, 1)

# Best fit line equation:
for x in x_data:
    y = (m * x) + b
    print(x, y)
1 5.04347826086957
5 6.608695652173917
8 7.7826086956521765
10 8.56521739130435

Cost & Loss - Mean Squared Error

image.png
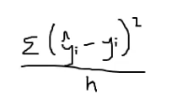
variable
x 1 5 8 10
y 4 8 9 7
y[hat] 5 6 7 8
cost 1 4 4 1 
# cost = (y[hat] - y) ^ 2 / 4

mse = 10 / 4
mse
2.5

Logistic Regression

image.png

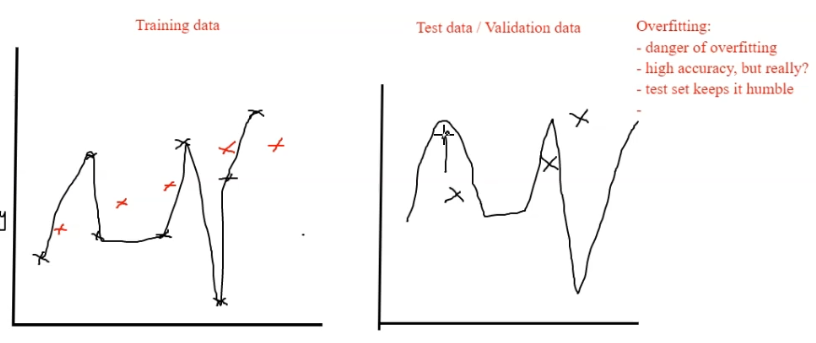
Overfitting

Best fit too accurately defines training data and minimizes the loss… but thats only training data and new data will keep the model humble.

image.png

image.png

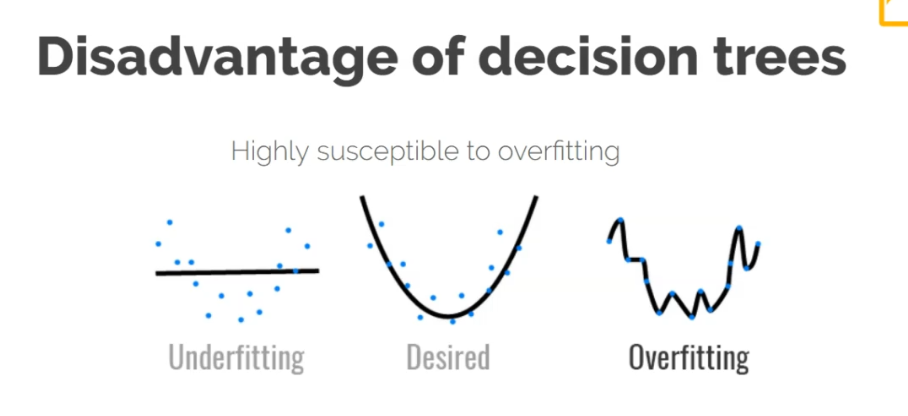
Random Forests

Random forests takes an average or majority decision from numerous decision trees and creates an output from this